
不静定構造物の解き方を教えて欲しい。

解き方は「応力法」と「変位法」がある
今回は応力法について解説するよ

曲げを受けるケースで考えてみよう。
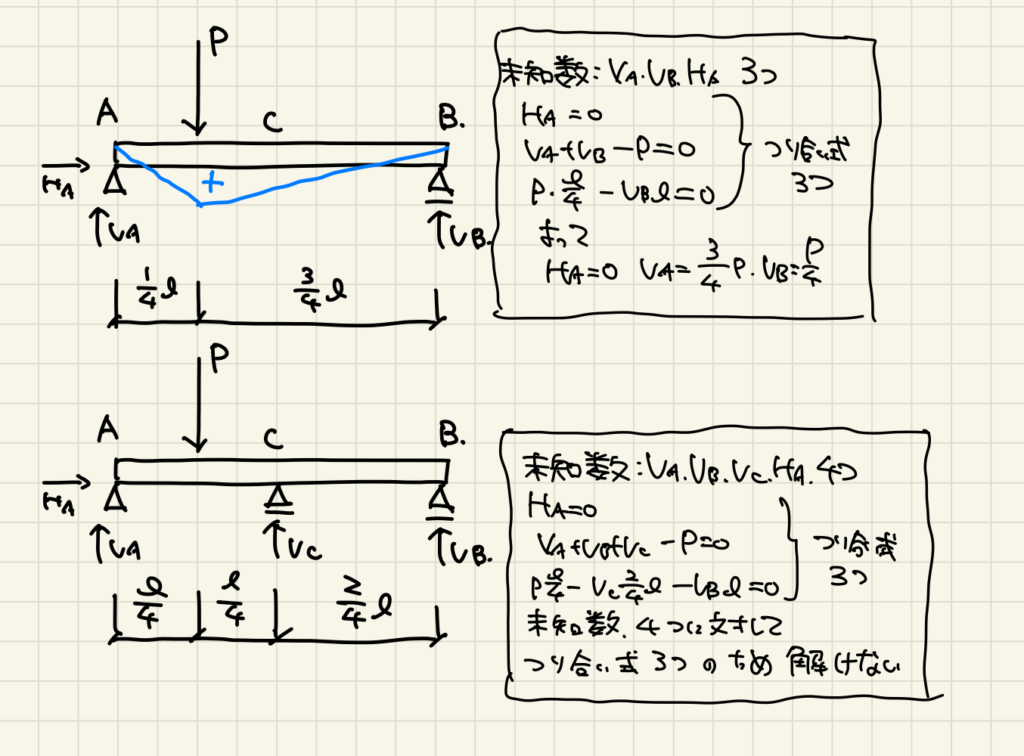
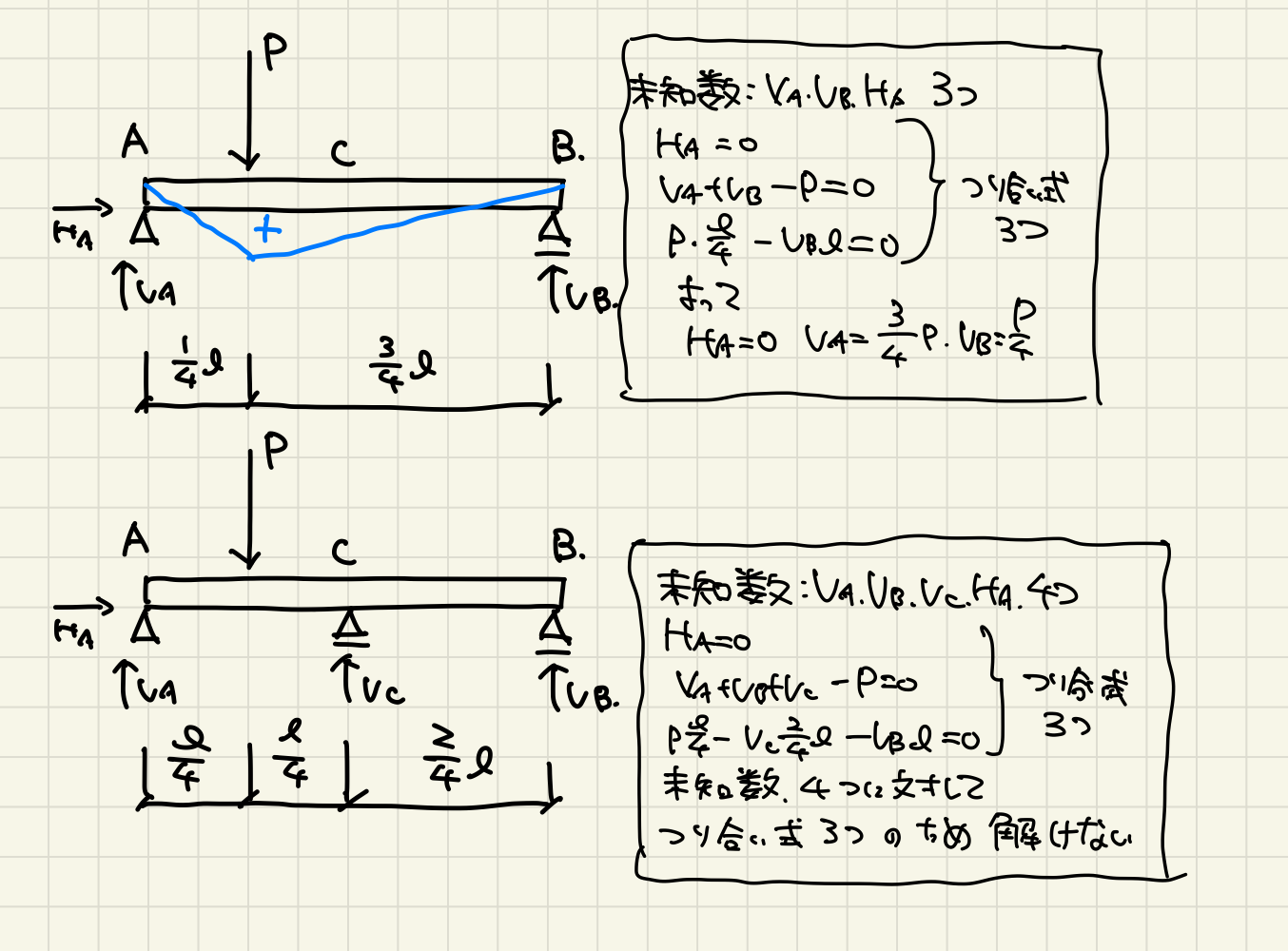
まず、下のイラスト上は反力数が3、つり合い式3と同じ数なので「静定構造物」
下のイラスト下は反力数が4、つり合い式が3と数が合わないので「不静定構造物」
このままではBを解けないので、「部材の変形」を考えてみる。

応力法のポイントは
まず、「支点を1つ外すなどしていったん静定構造として考えてみる」
静定構造物にするため、実際の構造物から条件を変更した、この仮の状態のことを
「静定基本形」というよ。

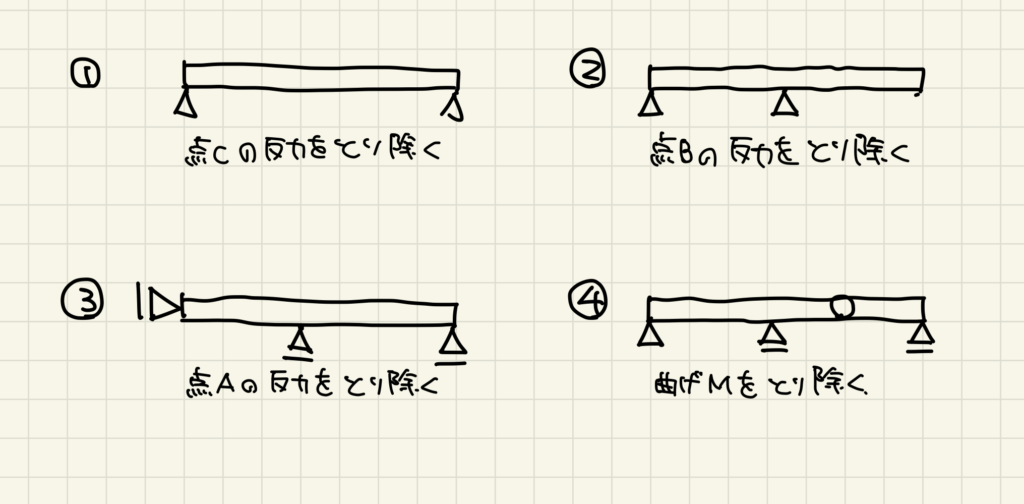
静定基本形の作り方
①中央の点Cの鉛直反力を取り除く
②点Bの鉛直反力を取り除く
③点Aのピン支点の鉛直反力を取り除く
④BC間の曲げモーメントを取り除く

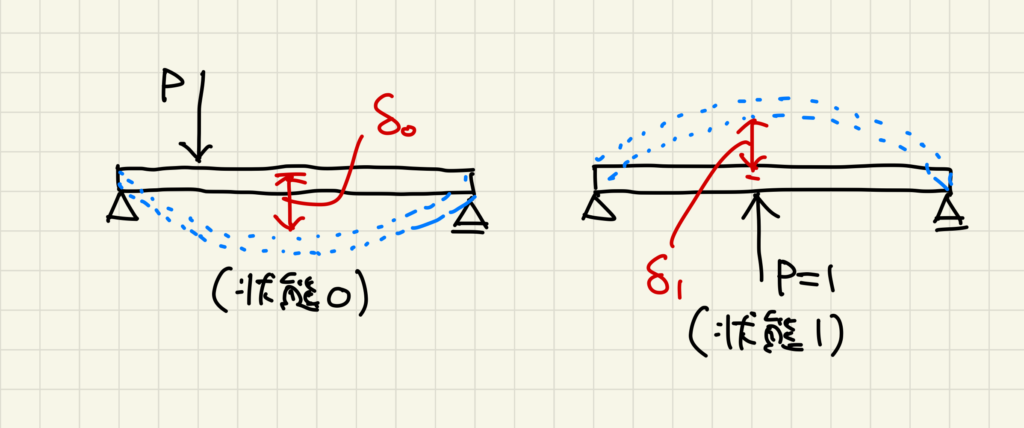
今回は①の方法で考えてみよう。
この時、必要なのは、点Cの鉛直変位だよ。この状態0
※変位は「単位仮想荷重法」や「モールの定理」を使えば求められる
これで、点Cの変形は求められたが、もともとの不静定構造物に戻ると
点Cは生じるはずのない変位が生じてしまっている。

これを0とするために
下から力を作用させて元に戻そうとしてみる。
どのくらいの力を作用させたらいいか分からないので
とりあえす単位荷重P=1の力で押してみて、その時の上向きの変位を求めてみる。
これを状態1

でも、状態0と状態1の変位を比較すると
一致していないよ

そだね
この段階では下から適当な荷重(P=1)を作用させただけだから
一致していないよ。

どのくらいの力を作用させたらいいの?

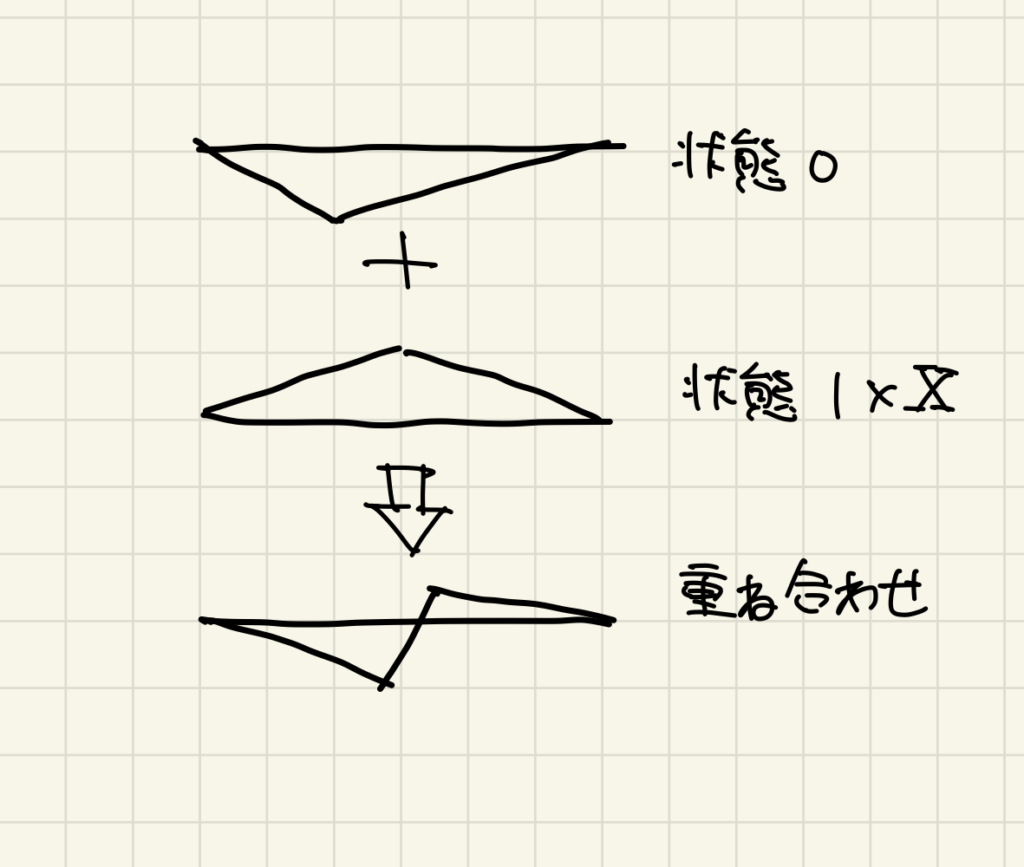
もともと変位0なので
δ0+Xδ1=0
っていう関係式になるよ。
これを変形すると
X=-(δ0/δ1)
ここでδ1は負の値なので
Xは正となる。
よって、P=1で下からXの力を作用させたら点Cの変位は0に戻る。
この状態はもとの不静定構造物の状態と同じである。
つまり、ここで求めることができた「Xは支点Cの鉛直反力と等しい」ことになる

応力法は比較的次数の少ない不静定構造物を解くのに適した方法だよ。
次数が3次以上となると、計算が煩雑になるから、たわみ角法などの別の方法がいいよ。


コメント